Основна основа за сва учења која познају свет јесте математику. Тачна наука користи формализовани језик и проучава редослед, структуру и односе на одабраним апстрактним објектима. Не воле сви ученици математику због ње сложеност и конфузија, али највероватније зато неразумевање. Трајне промене у односу на математику захтеваће посвећеност, концентрацију, доследност, чак тврдоглавост и, што је најважније, практична решења. У студији је важно корак по корак разумети једноставно и постепено прелазити на сложеније, не остављајући ништа неразумљиво и лоше замишљено.
Постоји много различитих грана математике које су довољно проучаване и појавиле се у последње време. Следеће су описане основе математичке анализе - основни почетни концепти, дефиниције и правила за проучавање једноставних функција једне променљиве, деривације и диференцијације.
Афоризам је настао код ученика основне школе: "Математика постаје заиста компликована када из ње нестану бројеви." Заправо се приближавају разумевању неких дефиниција и закона математичке науке одлучивањем о правилима користећи конкретне примере..
Кључне дефиниције
Кренимо од терминологије - са једноставним општим семантичким значењима примарних дефиниција:
- Вариабле - вредност или симбол, може узети било коју од више вредности у
специфична површина (тежина или висина детета)
- Функција - сврху, рад, активност, специфично деловање на променљивој, означавамо ф (к) (зависност тежине детета од његове висине)
- Лимит - граница, ивица, ивица (хоризонт - видно поље)
- Дериват - формирани, секундарни, који тече од другог, означавамо ф '(к) (брзина у кретању)
- Диференцијално - разлика, разлика, одвојеност.
Функција је праведна
Функција је резултат онога што ради са променљивом, а то је резултат израчуна. Ово је однос елемената у којем промена једне променљиве изазива промену друге. Поделите ф (к) на једноставне и сложене.
Следеће методе се користе за приказивање зависности: алгебарске, графичке, табеларне, логичке, па чак и софтверске.
Нумеричке зависности одређују се алгебрално коришћењем симбола променљивих, једнакости и неједнакости (≤ и>), конструише се једначина облика: и = ф (к), овде је к променљива или аргумент, а и или ф (к) је функција. За сваку специфичну вредност променљиве к из прихватљиве домене дефиниције одговара одређена вредност и за дати ф (к).
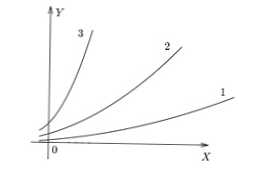
На слици испод приказани су једноставни графови у 3 различита односа. Може се видети да је у ф (к) 3 највећа вредност и добијена за к специфична, а у ф (к) 1 - најмања.
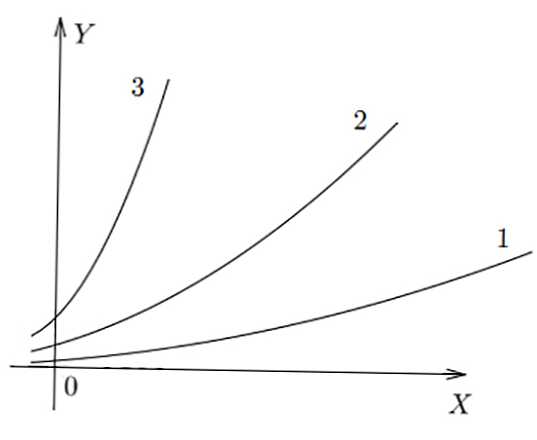
Функција
Разликују се следећи елементарни изрази: линеарни (директни), квадратни (парабола), кубични, хипербола, експоненцијални, логаритамски, тригонометријски (приказано у табели испод).
За анализу сваког типа ф (к) одређују се њихова својствена својства (наведена доле); за то се користе концепти деривативних и диференцијалних.
Деривативна функција
Дериват - оператера, који за оригинални ф (к) према законима диференцијације повезује другу функцију, она карактерише промену примарног ф (к) аргумента к у неком тренутку. Да бисмо га детаљно разумели, требало би да се позабавимо сложенијим дефиницијама границе зависности и диференцијације.
Лимит - ова дефиниција је динамична. Израз који к тежи ка н разуме се на следећи начин: к добија вредности које су близу н и разликују се по малом износу.
Диференцијално - мала промена неке величине. Повећање се назива делта.
Извод за ф (к) у тачки је граница дељења делте функције делта променљиве у датој тачки, ако последња тежи 0.
Карактеристика брзине промене зависности у одређеној тачки, геометријски се може приказати као тан вредност углова нагиба алфа тангенте на функцију.
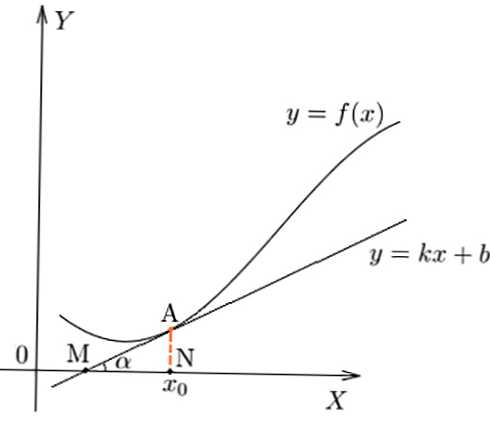
Дериват
Зависност се назива диференцибилном ако је дефинисан ф '(к). Проналажење деривата назива се диференцијацијом. Правила за израчунавање ф '(к) и подударања ф' (к) из елементарног ф (к) су дата у доњој табели
Изведена функција такође функционише
Свака зависност има одређена својства, знајући и истражујући их можете анализирати природу стања и промене ф (к).
Главне особине:
- Подаци о дефиницији и вредности разлике.
- Нула (к)
- Функција се повећава или смањује у неким интервалима.
- Показује МАКС и МИН функције, постоји ли прегиб.
- Пар или непар (ф)
- Ограничена и неограничена функција.
- Постоје ли асимптоте.
- Фреквенција ф (к).

Функције и деривати
При успостављању карактеристика зависности коришћењем деривата користе се међусобне везе својстава ф '(к) са својствима ф (к) и обрнуто. Карактеристике ф '(к) се лако одређују на графикону функције, и обрнуто, карактеристике примарног ф (к) се разумеју из графикона ф' (к). Поправљајући суштину сваке карактеристике функције, истражите и успоставите ланац односа. За одређивање асимптота у графовима користи се концепт ограничења..
Испод су неке карактеристике и зависности ф '(к) од ф (к):
- Како се ф (к) повећава у интервалу, ф '(к) је позитиван.
- Ако се ф (к) смањује током интервала, ф '(к) је негативан.
- У присуству ф (к) тачка МАКС, ф '(к) = 0 у њој се не може одредити, а тг угла тангенте мења се знак из + у -.
- У присуству ф (к) тачка МИН, ф '(к) = 0 у њој се не може одредити, а тг угла тангенте мења се знак из - у +.
- При савијању ф (к) у Е, вредност ф '(к) није променио знак у тачки, ф' (к) = 0.
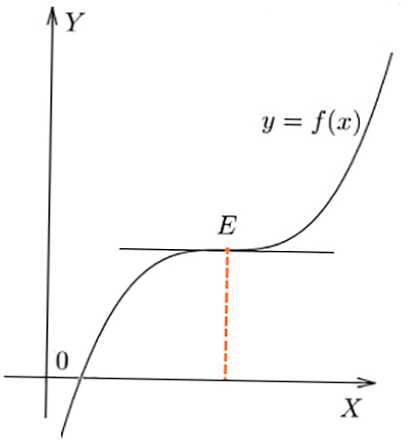
Флекција у тачки Е графикона функције
За истраживање, ф (к) сачињавају шему где је сваки корак конструисан према одређеном алгоритму за израчунавање и анализу односа компонентних елемената.
Разлике у функцијама и дериватима
Правила сабирања и одузимања ф (к) иста су као и правила ових акција током диференцијације. Али правила за проналажење ф '(к) под радњама множења и дељења функција су различита (као у табели).
Функција је примарна, а дериват је секундарна математичка операција, у већини случајева имају различите карактеристике.
Тачку непрекидне зависности сагиба се проналази њеним другим дериватом, а њен знак треба да се мења у региону тачке к0.
Постоје такве врсте функција које у тачки к0 (дисконтинуирано) немају ф '(к). У изражавању лн (| к | -1) дериват није дефинисан у тачки к0 = 1.
Постоје изрази "модуло" слично и = | к |, који има нагиб у к0.
За такве зависности, методе се користе само делимично (у интервалима домена дефиниције) за проучавање њихових својстава помоћу деривата и није увек могуће пребацити са својстава ф '(к) на својства.
Нигде се не може учинити без изузетака од правила, па чак ни у математици. Да бисмо анализирали и консолидовали представљени материјал, неопходно је решити примере, вежбати, стећи искуство с ограничењима, диференцијацијама и дериватима и храбро прећи на интеграле.











